So far we've seen:
- perspective is a set of conventions for representing depth, which nowadays mostly serves to evoke photography
- the perspective construction is based on a point called the 'centre of projection', and a specific image surface (a flat one, in rectilinear perspective)
- every point in a perspective drawing represents a distinct direction, travelling away from this centre of projection until it hits something, like a laser beam coming out of your eye
- if we look at a perspective drawing from anywhere other than the 'centre of projection', which is almost always the case, it may look distorted
- if we don't want these distortions for artistic effect, we should limit our field of view
There are two ways to go about making a perspective drawing. The first way is to be really meticulous and do everything very carefully with vanishing points. The second way is to just wing it: it will be ‘wrong’ but nobody will notice. However, it helps to practice the ‘right’ way to build the intuition that lets you do it the ‘fast’ way without anyone catching you without getting out a ruler.
Most of the time, when you do a meticulously accurate perspective drawing, what you’re gonna be drawing is a cuboid. Or at the very least, a flat, rectangular surface. If you’re drawing something else, you’ll probably start by projecting a rectangular grid, and then using that grid to help you draw the angular or curvy shape you actually wanted to draw.
So why do we like flat rectangular surfaces so much? This all comes back to the fundamental most important fact about perspective: if a collection of lines is parallel in 3D space, they all point towards the same, specific point in canvas space. This point is called the ‘vanishing point’ for that direction. We like rectangles because they have parallel sides, which we can point towards the same vanishing point.
You know earlier when we said that each point on the image corresponds to the direction of a laser beam coming out of your eye? Well, any line that points in the same direction as that laser beam in 3D space will point towards its vanishing point in canvas space. For example, imagine some logs are laid out like this:
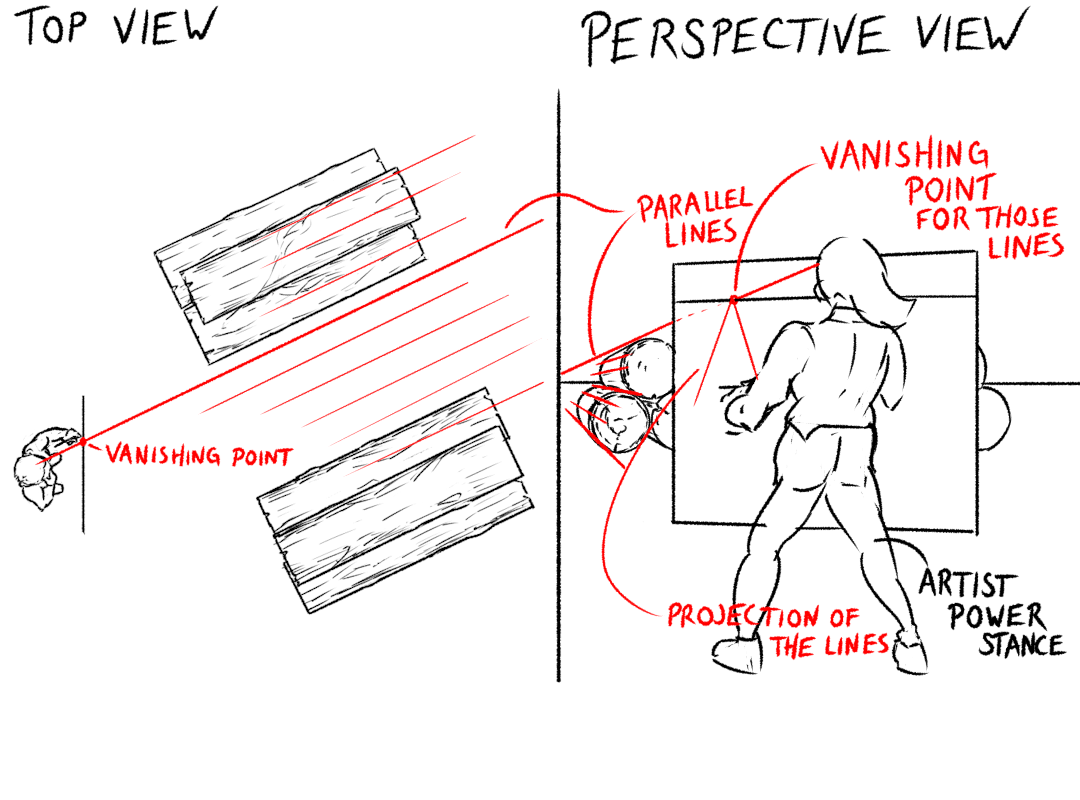
Shoot your eye laser out parallel to the logs. This will hit your canvas at a certain point; that’s your vanishing point. When you draw the logs, since they’re all parallel to that laser beam in 3D space, they all converge towards its vanishing point in canvas space:
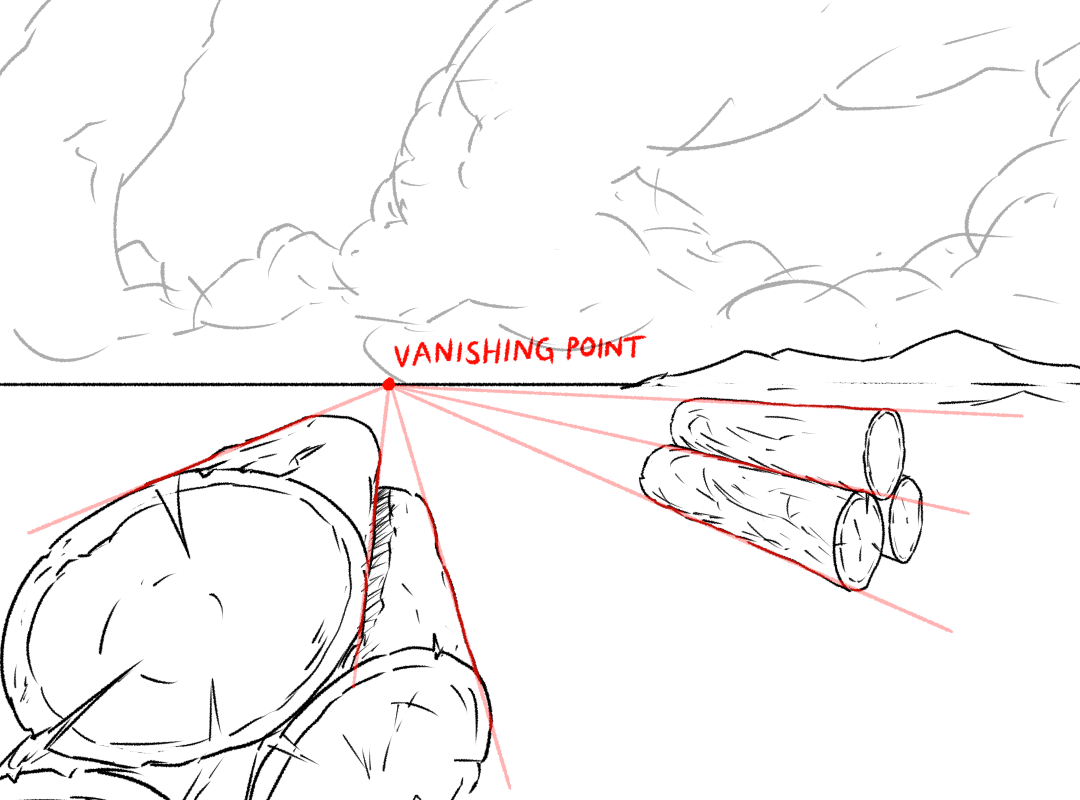
From this key perspective fact, basically all else follows!
We have one other technicality to clear up. As your eye lasers shoot out and hit the canvas, somewhere (possibly outside the actual canvas!) they will be hitting it ‘dead on’, perpendicular to the image plane.
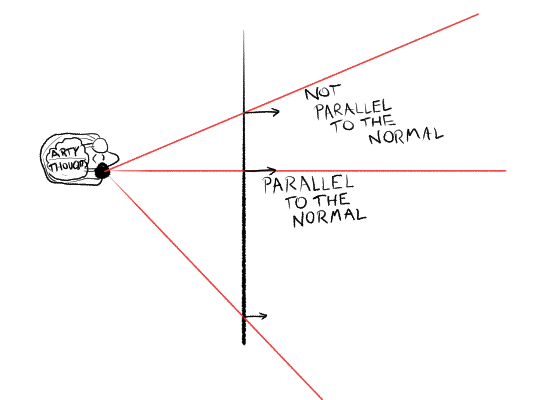
This ‘dead on’ direction is often singled out in perspective drawing, and sometimes referred to as the view direction, since if you have a camera, this is the direction it's pointing. However, I think that's a potentially confusing name, so instead I'm going to call it the canvas normal. ('Normal' in this context means 'perpendicular to a plane'.) Its vanishing point in canvas space is called the principal point. There’s nothing intrinsically special about this direction compared to the others, but it is very useful in a lot of perspective constructions.
As we saw in the previous article, if you want to minimise perspective 'distortion', you should make sure the principal point is near the centre of your picture. And if you want your drawing to look like it was taken with a camera, you should definitely put the principal point at the centre.
“How many” vanishing points
Perspective lessons often break things down into ‘one point’, ‘two point’ or ‘three point’ perspective. Though this scheme makes drawing simpler, I think it is a very artificial distinction.
Instead, I’d say there is one set of directions which are special: the ones which are parallel to the image plane. Imagine you shoot your eye laser exactly along the surface of your canvas. It will never hit it, even if you run it backwards out the back of your head as well. There is no vanishing point - or, equivalently, the vanishing point is infinitely far away.
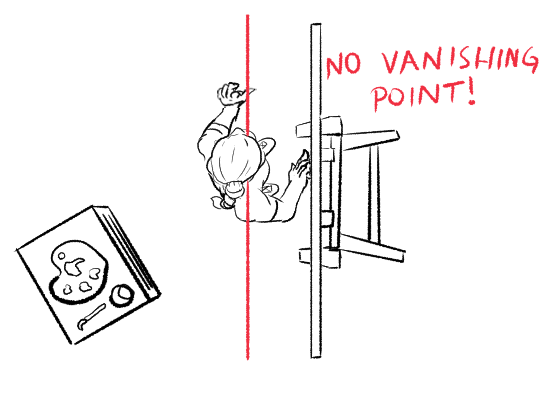
This means that if something is flat and parallel with the image plane, it has the same shape in canvas space as it does in 3D space!
If your canvas is vertical, which is to say if you are holding your camera level (as in ‘one’ or ‘two point’ perspective), then vertical lines in 3D space will be vertical on your canvas. This makes a lot of things less laborious to construct.
Now, suppose we want to draw a cube. A cube has three sets of edges, each of which will have a different vanishing point.
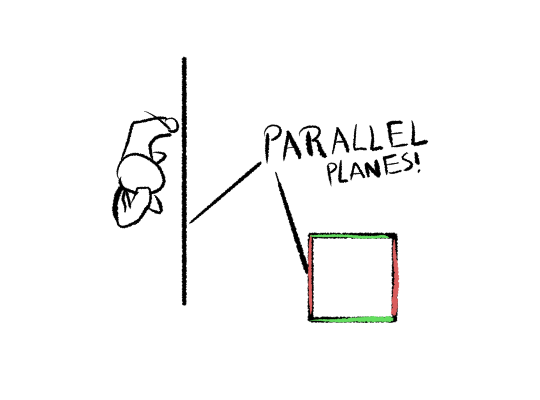
If we’re looking at it ‘end on’, by which I mean, looking at it so the nearest face is parallel to the image plane, that face will simply look like a square. We can see that in the render from earlier:
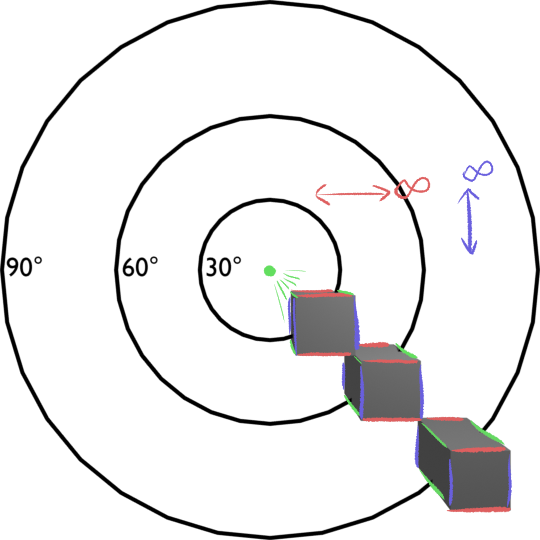
All three cubes have the same, equally sized square end; only the sides which aren’t parallel to the image plane look different when we move the cubes around!
Let's look at each set of parallel edges:
- The red and blue edges have infinitely distant vanishing points; they are parallel in canvas space.
- The green edges are parallel to the canvas normal in 3D space, so they all converge to its vanishing point in canvas space, the so-called 'principal point'. We placed that at the middle of the picture.
This setup is known as ‘one point’ perspective, since these cubes have exactly one vanishing point. Of course, if there were some cubes in the scene rotated to a different angle, they would have different vanishing points!
Most of the time we won’t meet the cubes ‘end on’. The main use for ‘one point’ perspective is when we’re looking down a long corridor or street. In this case, it’s pretty common to put the image plane perpendicular to the direction of the street.
OK, now let’s turn the cube around a bit. The vertical edges (blue) are still parallel to the image plane. But the other edges are not parallel to the image plane, so they’ll get vanishing points.
First, here it is from above:

And now, ‘two point’ perspective:

Here, the vanishing point for the red lines falls outside the 75-degree FOV of the image. The vanishing point for the green lines is inside the image. (Remember, these circles are marked with FOVs, not the angle from the central ray.)
Two point perspective is commonly used to show architecture in animation backgrounds. It can be seen as a default, neutral kind of shot; you are neither looking down (to diminish your subject or create a sense of vertigo) or looking up (to make your subject seem imposing or create a sense of grandeur).
Finally, ‘three point’ perspective shows cuboids where none of the faces are parallel to the image plane. In our everyday experience of the world, the vast majority of cuboids are in this condition. In this case, all three sets of lines have a vanishing point. Typically, your ‘camera’ is angled downwards:

The bad news is that a great deal of the time in a realistic composition, your cubes will be in this condition. The good news is that if you get good at drawing three point perspective, your pictures will really pop and appear impressively 3D. The tricky part is where to place the third vanishing point...
How far apart to place your vanishing points
When I first started trying to teach myself perspective drawing, the question of how far apart to place my vanishing points (in canvas space) was quite a headache. Nobody seemed to give the answer, beyond a vague admonition not to put them too close together.
This question is a matter of judgement, but hopefully what we’ve just seen can help us understand what we're actually deciding. Vanishing points represent directions; if we have a cuboid shape then its vanishing points are 90 degrees apart.
This means:
- if our vanishing points are close together, we have a wide-angle picture, like a wide-angle lens on a camera. perspective distortions will be very extreme.
- if our vanishing points are far apart, we have a narrow-angle picture, like a zoom lens. perspective distortions will be mild.
- if our vanishing points are infinitely far apart, we have an 'orthgraphic' rather than 'perspective' drawing, mostly used in diagrams. there are no perspective distortions at all.
However, it’s not so simple as ‘x distance on the paper = y degrees of view angle’. That would be true if we were drawing on the surface of a sphere, but we’re drawing on a flat piece of paper! Near to the ‘principal point', we’re looking at the paper straight on. When we look far away from that point, we’re glancing the paper at an oblique angle.
This means that angles are arranged in canvas space in an uneven way, like this:

(If you want to draw one of these yourself, the radius of a circle representing an angle \(\theta\) from the canvas normal is proportional to \(\tan\theta\).)
These angle circles can be used to measure the angles between eye lasers going through two different points, as long as the points are in a line with the principal point. Which is, admittedly, a pretty big limitation, but the circles help us get a sense of the layout of canvas space.
So if there’s 90 degrees separating two vanishing points, we could put them both on opposite sides of the 45° radius circle (since 45°+45°=90°). In this case, we’d get a perspective drawing like this:
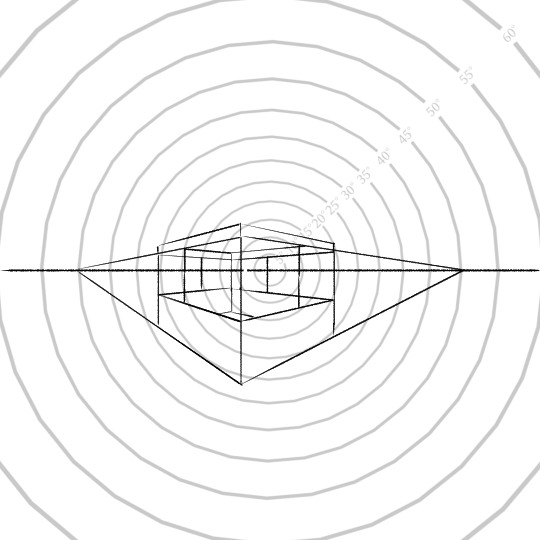
In this case, the vanishing points are 384 pixels apart. But suppose we rotated this around the vertical axis by 15 degrees. This moves one vanishing point onto the 30°-radius circle (since \(45\deg-15\deg=30\deg\)), and the other on the 60°-radius circle (since \(45\deg+15\deg=60\deg\)).
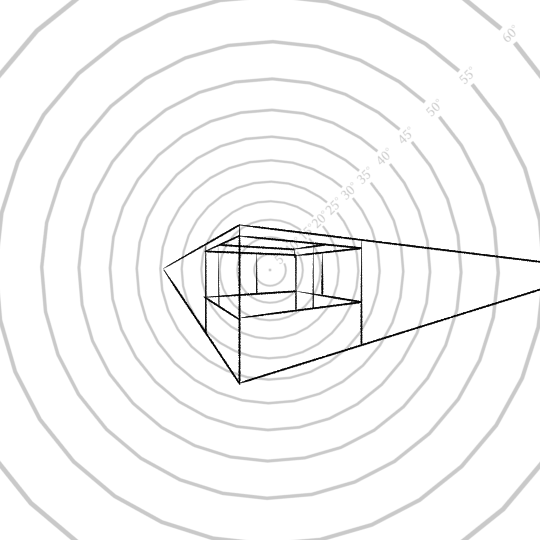
Does this mean you have to use a set of circles like this every time you draw in perspective? Not at all. Firstly, as we’ll discuss in the next section, it’s usually possible to eyeball perspective without doing a rigorous construction. But if you do want to do a rigorous construction, there is a method which I will cover in chapter 5, using the ‘90-degree circle', which lets you transform real angles you can measure with a protractor or set square into distances in canvas space. But before we get there, we need to build up some tools!
There is one other wrinkle. If you’re doing a full, three-point perspective, how do you make sure your third vanishing point is consistent with the lens angle implied by the other two? There is actually a fairly easy way to construct this, using the idea of a vanishing line, which we will also return to in chapter 5.
Winging it
Have a look at all those cubes we’ve rendered just now. Let’s notice some Rectangle Facts™:
- the faces of a cube, and rectangles in general, are always convex quadrilaterals (a needlessly fancy way to say ‘four-sided shapes’) in perspective, because straight lines in 3D space are also straight lines in canvas space
- these quadrilaterals taper off towards the vanishing points. opposite pairs of edges share a vanishing point.
- the more the rectangle is rotated perpendicular to the image plane in 3D space, the thinner it looks in canvas space. this is called foreshortening and we'll discuss it more later!
Fortunately for us, just about any convex quadrilateral could be a perspective projection of some rectangle. In fact, it could be the projection of a whole set of different rectangles, depending where the point of projection is sitting! Moreover, we humans are generally not great at figuring out whether it’s the right rectangle, as long as it’s near enough. In fact, the wrong projection might even look nicer sometimes.
Here are some convex quadrilaterals:
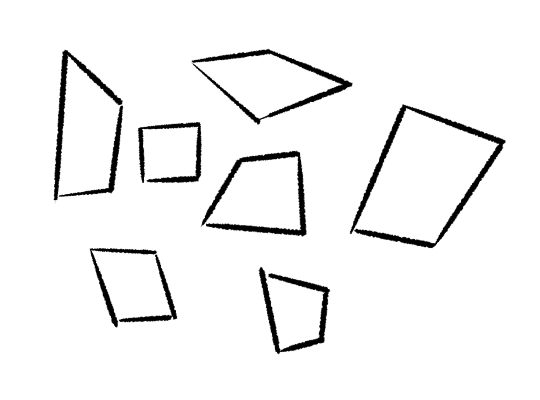
Any of these could a rectangle, projected in perspective. But which one do you pick for the rectangle you want to draw?
Let’s assume you’re starting with a square. Here’s how you figure out what it ought to look like:
- if we’re looking straight at it (i.e. near parallel to the image plane), all the sides are gonna be roughly the same length.
- if we’re glancing by it at an angle, it will look thinner, and it will taper (get narrower from one side to the other)
- how much does it taper? that basically depends how near the camera it is. if it’s a long way away, it will be very thin and not taper very much. if it’s nearby, it will be thicker, but also taper a lot.
In this animation, these three identical squares are spaced equally along a line in 3D space, and rotating at the same speed:
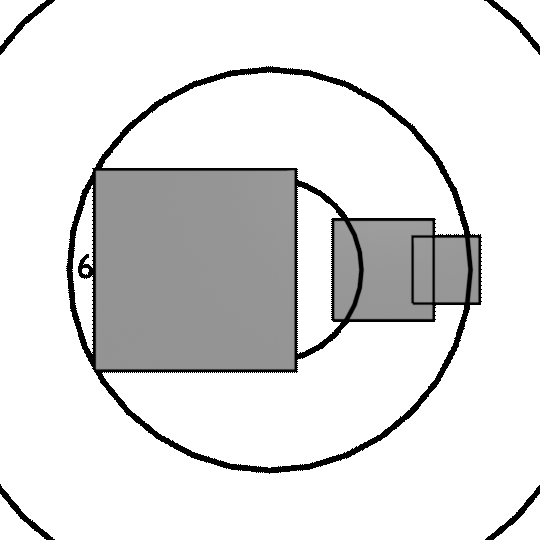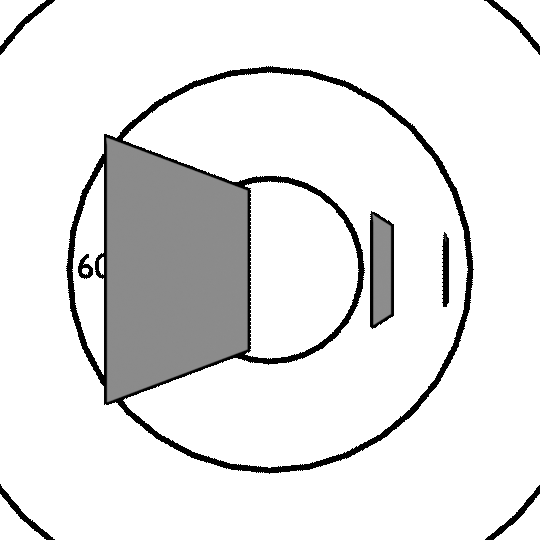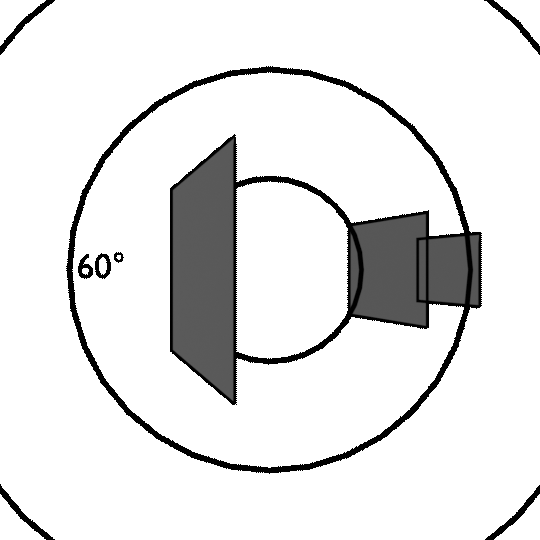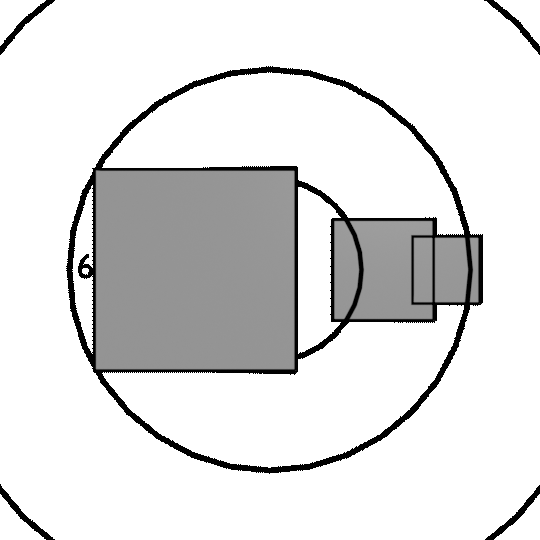
The one on the left is much nearer, and so it tapers a lot more when it turns.
Why should this be? It has to do with the way perspective usually compresses distances along the canvas normal much more for faraway objects than nearby objects.
It does what now?
Distance in perspective
Suppose you’re drawing a railway line. In 3D space, the railway sleepers are instantly far apart. But let’s have a look at what happens to them in perspective.
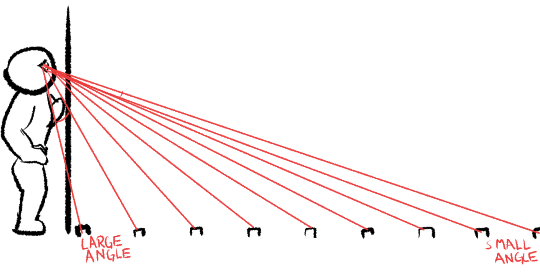
There are two effects here which are going to affect things. Firstly, let’s look at your eye lasers. Remember, perspective drawings represent the directions towards things. So since your eye lasers are wider apart for nearby things, the gaps between the nearby sleepers will appear to be bigger. We know this from everyday experience: far away things look small.
But there’s a second effect that compounds this. Notice that, for the nearby things, our eye lasers are hitting the canvas at a really oblique angle. This means the drawings of the two railways sleepers need to be even further apart in canvas space!
This is the reason why we try to keep the ‘principal point’, i.e. the point where our eye lasers are perpendicular to the image plane, near to the centre of the image, and limit the overall field of view. The viewer will probably not be sitting at the exact centre of projection, so these measures help avoid the distortions from looking too weird.
It also explains a general rough principle to keep in mind: stuff that’s near to you will look more ‘perspectivey’ than stuff that’s far away. Another way of looking at it: when stuff is nearby, the ‘near’ side will look much bigger than the far side of an object. When stuff is far away, the near and far sides will appear similar sizes, so it will look much closer to an ‘orthographic’ (non-perspective) projection.
This implies: if something is equally spaced in 3D space, it gets increasingly clustered in canvas space the further away it is.
Suppose you’re looking at a long street: the nearby buildings will take up lots of space in the frame. The faraway buildings will be reduced to slivers!
Now, how does this relate to our rotating squares? Consider a rotating object. As it rotates, one side gets nearer, the other gets further away. If the object is near the camera (point of projection), this leads to a much bigger change of shape in perspective space than if it’s a long way away.
Soon, we'll look at some more specific perspective tricks: how to build up relationships between the shapes we draw in perspective, to make sure your lines and planes are at the ‘right’ size and 'right' angles in relation to each other. But first, we have to meet planes and their vanishing lines.
Comments