Do planets close to the sun take more time to transit or less?

originally posted at https://canmom.tumblr.com/post/144133...

So yeah the transit of Mercury just happened, and I totally missed it. Oops. Not like I have a safe telescope projection rig anyway.

Nevertheless, this did make me wonder whether Mercury or Venus would take more time to transit.

Here’s some geometry, assuming a circular orbit for simplicity. We want to find the length of the orbital arc. \(x\) and \(y\) are angles because I couldn’t paste \(\theta\) and \(\phi\) into Inkscape for some reason. \(a\), \(r\) and \(l\) are known; the observer is stationary and coplanar with the circle.

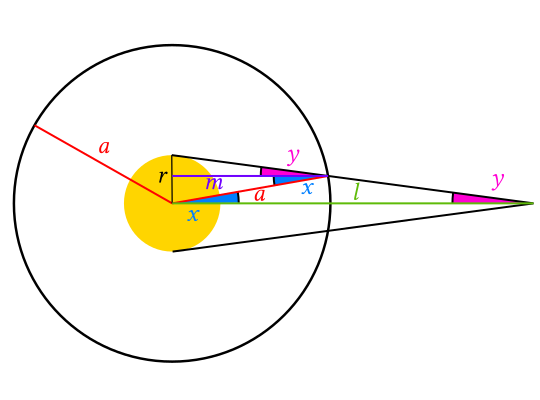
A complex diagram showing the geometry of a planetary transit. The sun is a circle of radius r at point S (unlabelled in the diagram), surrounded by a circular orbit of radius a. The observer is a point O on the right. The sun subtends an angle 2y at the observer. The line from the observer intercepts the circular orbit at a certain point, P (unlabelled in the diagram). The angle OSP is labelled x. An additional line of length m is drawn, parallel to the line SO, connecting point P to a line from O perpendicular to SO. I'm extremely sorry if you're using a screen reader.

So, peering at this diagram we say $$l \tan y = r$$ and also $$a \cos x = m$$ and also that $$m( \tan y + \tan x )=r$$ and the arc length is \(2ax\) (where \(x\) needs to be in radians of course).

OK, so let’s combine some things: $$a \cos x \left(\frac{r}{l}+\tan x\right)=r$$and that will allow a little rearrangement to $$\frac{ \cos x }{l} + \frac{\sin x}{r} = \frac{1}{a}$$

Well that’s like, probably impossible to solve analytically, but look we’re on a computer.

First of all here’s the angle \(x\):

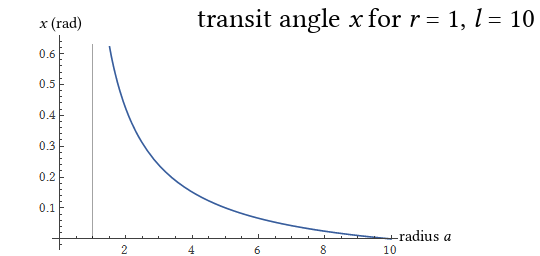
The angle x from the previous diagram over a range of orbital radii a when r=1 and l=10. There is a singularity at a=r, and x is 0 when a=l.

So yeah \(x\) gets bigger as the orbit gets tight around the sun. I guess ultimately it’s going to go all the way up to \(\frac{\pi}{2}\) but Mathematica didn’t to show me that and it’s not important enough to fiddle around with Exclusions->None and all that.

OK let’s also check out the arc length

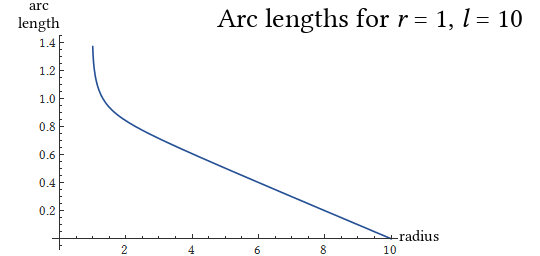
The length of arc on an orbit during which a planet is transitting the sun, plotted for various values of a. The plot is linearly decreasing from about a=2 to a=10, but below a=2 it increases sharply towards an asymptote at a=1.

So the arc length is big when you’re in a really tight orbit round the sun, and otherwise just pretty much linearly decreases out towards the observer. cool

OK how much time does it take to cross this cone of vision? let’s grab Kepler. Kepler’s laws, which describe the motion of planets, say the square of the time it takes to go round the orbit (which we’ll call \(T\)) is proportional to the cube of the semi-major axis \(a\), which for a circular orbit is just the radius of the orbit. Neat. So that says $$T^2 \propto a^3$$

Of that time \(T\), a time \(t=\frac{Tx}{2\pi}\) is spent inside the transit visibility cone. That means $$t \propto x a^\frac{3}{2}$$ so let’s plot that thing.

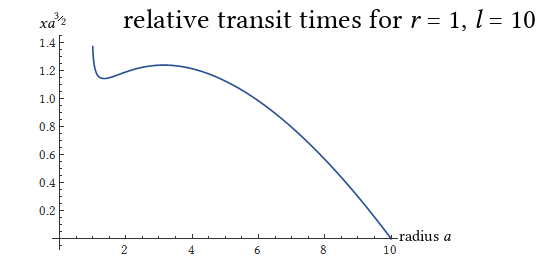
'Relative transit times' plotted for various values of a with r=1 and l=10, representing a value proportional to the amount of time spent transiting the sun. There is a singularity at a=1, and a local maximum around a=3, before falling to zero at a=l=10.

So it looks like close to the sun is generally better, but there’s a local maximum some distance away from the sun. OK, what happens if we plot this in terms of more realistic relative sizes, i.e., set \(a\) to 1AU and \(r\) to the radius of the sun?

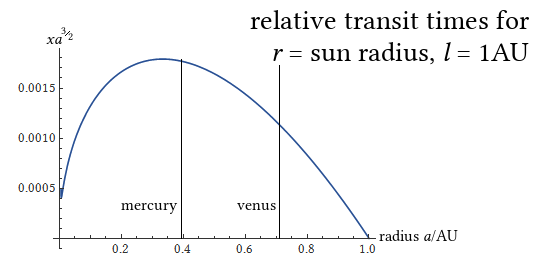
'Relative transit times' plotted with physical values of r = 1 solar radius and l = 1 AU. The semi-major axes of the orbits of Mercury and Venus are plotted as vertical lines. There is a local maximum around 0.3 AU, which is just inside the orbit of Mercury.

The hump is much bigger! And apparently for us Earth observers (or rather, a stationary observer at the orbit of Earth observing a coplanar circular orbit), the sweet spot is around 0.3AU.

Anyway that’s our answer for where it’s best to be if you want to spend a long time transiting the sun. Also, Mercury has a longer transit time than Venus. In reality it’s more complicated because orbits are elliptical and not coplanar, and the Earth moves during the transit too, so you only get transits sometimes and the time is a bit more complicated to calculate.

Comments

Add a comment
[?]